ABSTRACT
Wind induced (aeolian) vibrations of
conductors and overhead shield wires
(OHSW) on transmission and distribution lines
can produce damage that will negatively
impact the reliability or serviceability of these
lines. Lines damaged by vibration may have to
be de-rated or even taken out of service until
repairs can be made. This could have an
impact on an entire network.
Understanding aeolian vibration and how it
can be managed or controlled is the key to
minimizing its possible effect on a line or
network.
This report will present an executive summary
of the research and findings of industry
experts all over the world who have
contributed to the understanding of aeolian
vibration and its control. The references cited
will provide a more detailed explanation of
individual principles, findings and
recommendations
MECHANISM OF AEOLIAN VIBRATION
When a “smooth” stream of air passes across
a cylindrical shape, such as a conductor or
OHSW, vortices (eddies) are formed on the
leeward side (back side). These vortices
alternate from the top and bottom surfaces,
and create alternating pressures that tend to
produce movement at right angles to the
direction of the air flow. This is the mechanism
that causes aeolian vibration [1].
The term “smooth” was used in the above
description because unsmooth air (i.e., air with
turbulence) will not generate the vortices and
associated pressures. The degree of
turbulence in the wind is affected both by the
terrain over which it passes and the wind
velocity itself. It is for these reasons that
aeolian vibration is generally produced by
wind velocities below 15 miles per hour
(MPH). Winds higher than 15 MPH usually
contain a considerable amount of turbulence,
except for special cases such as open bodies
of water or canyons where the effect of the
terrain is minimal.
The frequency at which the vortices alternate
from the top to bottom surfaces of conductors
and shield wires can be closely approximated
by the following relationship that is based on
the Strouhal Number [2].
Vortex Frequency (Hertz) = 3.26V / d
where: V is the wind velocity component
normal to the conductor or OHSW
in miles per hour
d is the conductor or OHSW
diameter in inches
3.26 is an empirical aerodynamic
constant
One thing that is clear from the above
equation is that the frequency at which the
vortices alternate is inversely proportional to
the diameter of the conductor or OHSW.
For example, the vortex frequency for a 795
kcmil 26/7 ACSR (“Drake”) conductor under
the influence of an 8 MPH wind is 23.5 Hertz.
A 3/8” OHSW under the same 8 MPH wind will
have vortices alternating at 72.4 Hertz. The
fact that the vortex frequency for an OHSW is
much higher than that for a conductor will be
important to remember when the effects of
vibration are discussed later in this report.
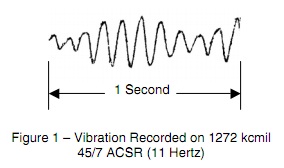
To further illustrate the difference in vibration
frequencies between conductor and OHSW,
Figures 1 & 2 show actual vibration recordings
made on a line in the western part of the U.S.
The recordings were taken with an Ontario
Hydro Recorder on a 1400’ span. The
conductor is 1272 kcmil 45/7 ACSR (“Bittern”)
and the OHSW is 3/8” EHS. Plugging the
recorded frequencies and diameters into the
above equation yields the same apparent wind
velocity (4.5MPH) for both the conductor and
OHSW.
Sustained aeolian vibration activity occurs
when the vortex frequency closely
corresponds to one of the natural vibration
frequencies of the span of conductor or
OHSW. This sustained vibration activity takes
the form of discrete standing waves with
forced nodes at the support structures and
intermediate nodes spaced along the span at
intervals that depend on the particular natural
frequency (Figure 3).
The natural frequencies at which a conductor
or OHSW under tension will vibrate in a series
of standing waves are approximated by:
F = (Tg/w)
1/2
x N/2S
where:
F is the natural frequency in hertz
T is the tension in pounds
g is the gravitational constant of 32.2 ft/sec
2
w is the conductor or OHSW weight per foot
N is the number of standing wave loops
S is the span length in feet
For example, the natural frequencies for an
800’ span of 795 kcmil 26/7 ACSR (“Drake”)
conductor at a tension of 4,725# are given by:
F = 0.233 x N
It was stated earlier that sustained vibration
will occur when the vortex shedding frequency
of the wind is equal to one of the natural
frequencies of the span. Therefore, for this
example, using 800’ of Drake conductor at a
tension of 4,725#:2.9422 x V = 0.233 N
or
12.6275 x V = N
For a wind velocity of about 8 MPH, the span
in this example would have 100 standing
waves (N=100), each about 8’ in length (loop
length). At a higher wind speed near 12 MPH
the loop length will decrease to 5.3’ (N=150).
The importance of loop lengths will be
discussed in a later section dealing with the
placement of dampers.
The amplitude at which a span will vibrate
(peak-to-peak movement at the anti-node in
Figure 3) depends on a number of factors
which include the energy that is transferred to
the span by the wind and the amount of
damping in the span from the conductor or
OHSW itself (self damping) or from additional
dampers installed in the span.
In most cases the maximum peak-to-peak
amplitude of a vibrating conductor or OHSW
will not exceed its diameter.
Extensive research utilizing wind tunnel
studies has been used to determine the
energy imparted by the wind to a vibrating
conductor [3], [4], [5], [6], [7], [8], [9].
Collectively this research has shown that wind
energy may be expressed in the general (nonlinear) form:
P = L x d4 x f3 x fnc(Y/d)
where:
P is the wind energy in watts
L is the span length
d is the conductor diameter
f is the vibration frequency in hertz
Y is the anti-node vibration (peak-to-peak)
fnc(Y/d) is a function derived from
experimentation
The above expression assumes completely
laminar wind flow, free of turbulence. The
effects of turbulence will be discussed later in
this report.
The self damping characteristics of a
conductor or OHSW are basically related to
the freedom of movement or “looseness”
between the individual strands or layers of the
overall construction. In standard conductors
the freedom of movement (self damping) will
be reduced as the tension is increased. It is for
this reason that vibration activity is most
severe in the coldest months of the year when
the tensions are the highest.
Some conductors designed with higher self
damping performance use trapezoidal shaped
outer strands that “lock” together to create
gaps between layers. Other conductors, such
as ACSS (formerly SSAC), utilize fully
annealed aluminum strands that become
inherently looser when the conductor
progresses from initial to final operating
tension.
Procedures have been established for
measuring self damping performance of
conductors and OHSW in the laboratory [10].
The energy absorbed by damping devices
added to a span of conductor or OHSW is the
subject of a later section of this report.
EFFECTS OF AEOLIAN VIBRATION
It should be understood that the existence of
aeolian vibration on a transmission or
distribution line doesn’t necessarily constitute
a problem. However, if the magnitude of the
vibration is high enough, damage in the form
of abrasion or fatigue failures will generally
occur over a period of time.
Abrasion is the wearing away of the surface of
a conductor or OHSW and is generally
associated with loose connections between
the conductor or OHSW and attachment
hardware or other conductor fittings. The
looseness that allows the abrasion to occur is
often the result of excessive aeolian vibration.
Abrasion damage can occur within the span
itself at spacers (Figure 4), spacer dampers
and marker spheres, or at supporting
structures (Figure 5).

FIG5
Fatigue failures are the direct result of bending
a material back and forth a sufficient amount
over a sufficient number of cycles. Removing
the pull tab from a can of soda is a good
example.
All materials have a certain “endurance limit”
related to fatigue. The endurance limit is the
value of bending stress above which a fatigue
failure will occur after a certain number of
bending cycles, and below which fatigue
failures will not occur, regardless of the
number of bending cycles.
In the case of a conductor or OHSW being
subjected to aeolian vibration, the maximum
bending stresses occur at locations where the
conductor or OHSW is being restrained from
movement. Such restraint can occur in the
span at the edge of clamps of spacers, spacer
dampers and stockbridge type dampers.
However, the level of restraint, and therefore
the level of bending stresses, is generally
highest at the supporting structures.
When the bending stresses in a conductor or
OHSW due to aeolian vibration exceed the
endurance limit, fatigue failures will occur
(Figure 6). The time to failure will depend on
the magnitude of the bending stresses and the
number of bending cycles accumulated [11],
[12], [13].
In a circular cross-section, such as a
conductor or OHSW, the bending stress is
zero at the center and increases to the
maximum at the top and bottom surfaces
(assuming the bending is about the horizontal
axis). This means that the strands in the outer
layer will be subjected to the highest level of
bending stress and will logically be the first to
fail in fatigue.
The same principle applies to the addition of
Armor Rods to the conductor or OHSW at
support locations. A portion of the bending
stress is applied to the Armor Rods, which
reduces the bending stress on the conductor
or OHSW. Since the Armor Rods are located
the furthest from the center line of the
conductor, they will be subjected to the
highest level of bending stress, and would be
expected to fatigue before the conductor
strands. However, with the use of bolted
suspension clamps this is not the usual mode
of failure (Figure 7).

The reason that a conductor will fail under
Armor Rods is that the bolted suspension
clamp produces a substantial amount of
compression load when it is installed. The
compression between the keeper and the
clamp body somewhat “crushes” the
conductor (Figure 8).
The compression force produces notches in
the aluminum strands of conductors as they
pass over each other (the strands in each
layer are produced in the opposite lay
direction). The resulting notches (Figure 9)
create stress risers that substantially reduce
the endurance limit of the affected strands.
It is clear that care must be taken when
removing Armor Rods from a line that has
been subjected to moderate or severe aeolian
vibration activity.
Suspension assemblies, such as the
ARMOR-GRIP® Suspension and the
CUSHION-GRIP™ Suspension which use
elastomer cushions, with or without factoryformed rods, hold the conductor with a
minimal amount of compression force
(Figure 10).
The conductor in the elastomer cushions
bends gradually, compared to the abrupt
bending at the edge of a bolted clamp’s
keeper, and notching of the aluminum strands
does not occur. The net result is that a
conductor or OHSW in a suspension assembly
that uses elastomer cushions can withstand
higher levels of aeolian vibration activity
without fatigue failure.SAFE DESIGN TENSION WITH RESPECT
TO AEOLIAN VIBRATION
There are a number of factors taken into
account in choosing a design tension for a
transmission or distribution line. These factors
include:
• Average Span Length
• Overall Height of Structures
• Maximum Tension at Highest Wind
and/or Ice Loading
• Clearances at Highest Operating
Temperature
• Susceptibility to Aeolian Vibration
Of these factors the susceptibility to aeolian
vibration has been the only one that is difficult
to quantify. Beginning in the early 1960s, and
based on available field experience at that
time, the industry adopted a “rule of thumb” for
safe design tensions with respect to aeolian
vibration [14]. It was suggested that the
everyday stress (EDS) be limited to 18% of
the conductor rated breaking strength (RBS)
to assure safe operation with regard to aeolian
vibration. More recent surveys of the
performance of actual lines [15] that had been
in service for 10 to 20 years revealed that up
to 45% of lines installed using an EDS <18%
experienced fatigue failures. A new guideline
was clearly needed.
The work that led to the publishing of CIGRE
Report #273, “Overhead Conductor Safe
Design Tension With Respect To Aeolian
Vibrations” in June, 2005 [15] was based on
the ratio of the horizontal conductor tension,
H, and the conductor weight per unit length, w.
The effects of terrain on the turbulence
intensity of the wind were also studied and
included as part of the overall
recommendations.
The horizontal conductor tension used to
calculate the H/w ratio is the initial, unloaded
tension at the average temperature of the
coldest month at the location of the line.
By applying the H/w ratio and the newly
created terrain categories to all available field
experience data, the CIGRE Task Force
published the recommendations shown in
Table 1 for single undamped, unarmored
conductors. The Task Force also published
the warning that the recommendations “should
be suitable most of the time” but that “special
situations require specific attention”. “Extralong spans, spans covered with ice, rime or
hoarfrost, spans equipped with aircraft warning
devices, and spans using non-conventional
conductors” were examples cited of special
situations.
CIGRE Report #273 also provides
recommendations for safe design tensions for
bundled (twin, tri and quad) conductors.
INFLUENCE OF SUSPENSION HARDWARE
The use of Armor Rods (Figure 11) or high
performance suspension assemblies (Figures
12 & 13) reduces the level of dynamic bending
stress on a vibrating conductor.
As reported earlier Armor Rods will absorb a
portion of the bending stress at the edges of
the suspension clamp, but do nothing to
reduce the effects of the compression loading
and resulting notching of the aluminum
strands.
Consequently, there is negligible influence of
Armor Rods on the recommendations for safe
design tensions (with or without dampers).
The use of elastomer cushions on high
performance suspensions, such as the AGS
and CGS, provide two benefits. First, within
the elastomer cushion the vibrating conductor
is bent in a gradual manner along the cushion,
rather than bending abruptly at the edge of a
metallic keeper (suspension clamp).
Secondly, the elastomer cushions, with or
without externally applied rods (as with the
AGS) minimize or eliminate the compression
loading on the conductor, which causes
notching of the aluminum strands.
As a result high performance suspensions will
allow higher safe design tensions (H/w) and
have a positive influence on the “protectable”
span length of a damper.
The amount of positive influence and
additional protection provided by performance
suspensions is difficult to reduce to a simple
table. Contact PLP with specific line design
and environmental (terrain and temperatures)
data for more information.